Atomic structure

Aims of this section
After studying this section, you should be able to:
- describe how the atomic model has changed over time
- recall atomic structure in terms of the positions and properties of subatomic particles
- calculate the numbers of subatomic particles in isotopes from atomic numbers and mass numbers
- calculate relative atomic masses.
Summaries
Development of the atomic model
Our understanding of atomic structure has developed over time. The diagrams show some important atomic models.
Atoms consist of subatomic particles. The table shows their locations in atoms, relative masses and relative charges.
| Proton | Neutron | Electron | |
|---|---|---|---|
| Location | nucleus | nucleus | shells (energy levels) |
| Relative charge | +1 | 0 | –1 |
| Relative mass | 1 | 1 | 1⁄1836 |
Atomic number, mass number and isotopes
Atomic number is the number of protons in the nucleus.
Mass number is the total number of protons and neutrons in the nucleus.
You can calculate the number of particles in an atom from these two numbers:
- number of protons = atomic number
- number of neutrons = (mass number) – (atomic number)
- number of electrons = number of protons
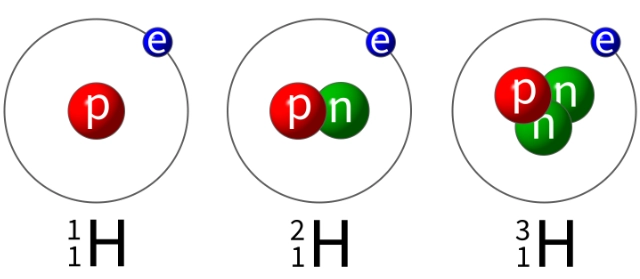
Isotopes of an element are different atoms with:
- the same number of protons but different numbers of neutrons in their nuclei
- the same atomic number but different mass numbers.
Isotopes of an element have identical chemical properties. The existence of isotopes explains why relative atomic masses are not whole numbers (unless they are rounded up or down).
Calculating relative atomic mass
The relative atomic mass of an element is the weighted mean mass of its atoms compared to 1⁄12th the mass of a 12C atom. It is given the symbol Ar.
You can often find Ar values on periodic tables, but take care – they are not mass numbers.
You can calculate the relative atomic mass of an element if you know:
- the mass numbers of its isotopes
- the percentage abundance of each isotope.
Worked example
A sample of chlorine contains two different isotopes, as shown in the table. Calculate the relative atomic mass of chlorine.
| Isotope | Mass number | Percentage abundance |
|---|---|---|
| 35Cl | 35 | 75 |
| 37Cl | 37 | 25 |
Answer
[katex]\displaystyle\footnotesize\textsf{relative atomic mass = }\frac{(35\times75)+(37\times25)}{(75+25)}[/katex]
[katex]\displaystyle\footnotesize\textsf=\frac{2625+925}{100}=\frac{3550}{100}=35.5[/katex]

The periodic table shows that chlorine has an Ar of 35.5, rather than 35 or 37. The value is closer to 35 than to 37 because most chlorine atoms are 35Cl atoms rather than 37Cl atoms.
