Relative atomic mass

Aims of this page
After studying this page, you should be able to:
- recall what is meant by relative atomic mass
- calculate relative atomic masses from isotopic abundances.
What is relative atomic mass?
Relative atomic masses have no units. This is because they are comparisons. You do not need to know the actual masses of atoms to use relative atomic masses. This is just as well because the mass of a 12C atom is only 1.99 × 10–26 kg.

You can only know the mass number of an atom if you:
- are given it, for example in a question, or
- analyse its isotopic symbol.
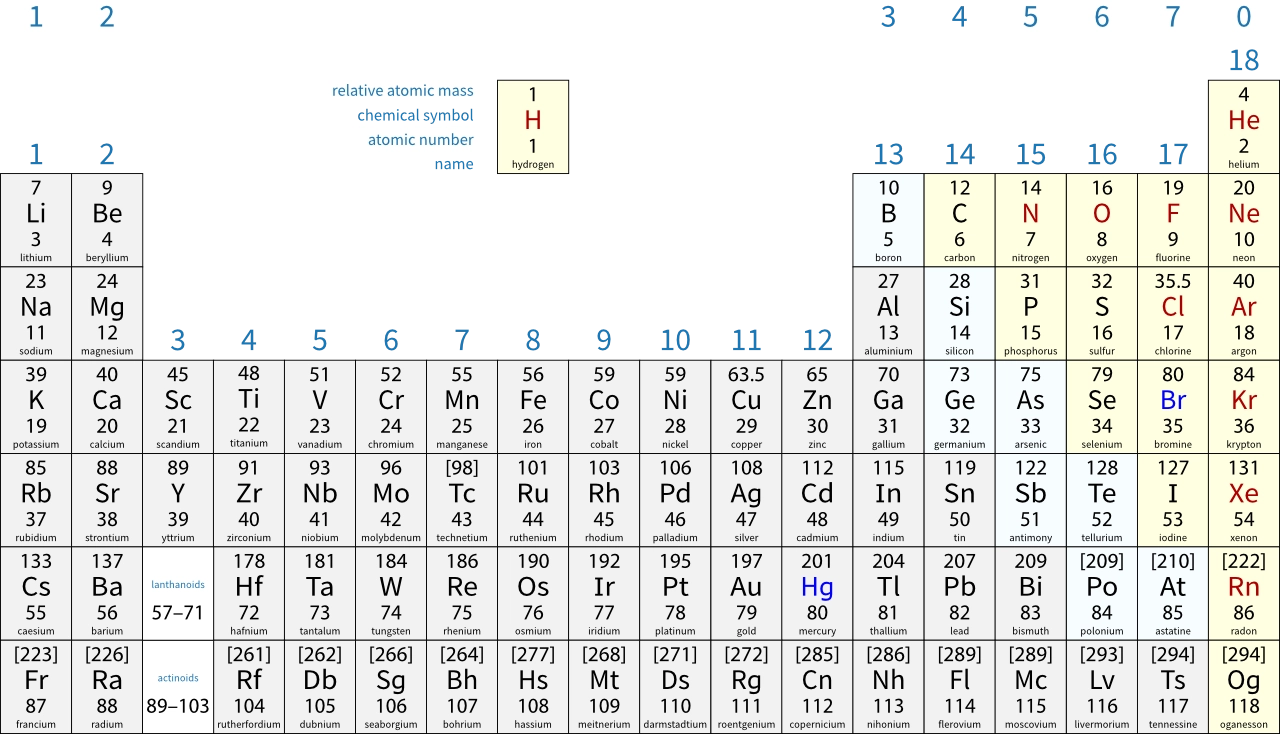
For example, the mass number of \(\ce{^{7}_{3}\displaystyle\small\textsf{Li}}\) is 7. This happens to be the Ar for lithium, as shown in the periodic table below. However, the Ar for lithium is actually 6.94 because:
- lithium consists of two isotopes, \(\ce{^{6}_{3}\displaystyle\small\textsf{Li}}\) and \(\ce{^{7}_{3}\displaystyle\small\textsf{Li}}\), and
- the value in the periodic table above is rounded to the nearest whole number.
The periodic table used in the OCR GCSE specification shows all relative atomic masses to 1 decimal place (and at the bottom of each box rather than at the top). In this periodic table, the relative atomic mass of lithium is shown as 6.9 because it has been been rounded to 1 decimal place rather than to a whole number.
Calculating relative atomic mass
You can calculate the relative atomic mass of an element if you know:
- the mass numbers of its isotopes
- the percentage abundance of each isotope.
This is Higher Tier only in some GCSE specifications – check yours.
Worked example
A sample of bromine contains two different isotopes, as shown in the table. Calculate the relative atomic mass of bromine. Give your answer to 1 decimal place.
| Isotope | Mass number | Percentage abundance |
|---|---|---|
| 79Br | 79 | 50.7 |
| 81Br | 81 | 49.3 |
relative atomic mass
\(\ce\displaystyle\large\textsf=\frac{(79\times50.7)+(81\times49.3)}{(50.7+49.3)}\)
\(\ce\displaystyle\large\textsf=\frac{4005.3+3993.3}{100}=\frac{7998.6}{100}\)
= 80.0 (to 1 decimal place)

The periodic table shows that bromine has an Ar of 80, rather than 79 or 81. The value is half-way between 79 and 81 because about half the bromine atoms are 79Br and about half are 81Br.
